SIT718 Real world Analytics Assignment - Deakin University, Australia

EXPERTSMINDS.COM GIVES ACCOUNTABILITY OF YOUR TIME AND MONEY - AVAIL TOP RESULTS ORIGINATED SIT718 REAL WORLD ANALYTICS ASSIGNMENT HELP SERVICES AT BEST RATES!

Question 1 -

a) Explain why a linear programming model would be suitable for this case study.

b) Formulate a Linear Programming (LP) model for the factory that minimises the total cost of producing the beverage while satisfying all constraints.

c) Use the graphical method to find the optimal solution. Show the feasible region and the optimal solution on the graph. Annotate all lines on your graph. What is the minimal cost for the product?

d) Is there a range for the cost ($) of A that can be changed without affecting the optimum solution obtained above?

Answer -

(a) Why linear programming is suitable for this problem

The information given in this question indicates that a LPP is appropriate. The objective function is linear equation and the 3 constrains can are possible linear inequalities.

(b) Model formulation

Step 1: Decision variables

This step involves identifying what variables we need to control in order to achieve optimal solution (minimum cost of production for this case). Here we are mixing two types of products, product A and B, so we only have control over A and B. the decision variables are;

A = Amount of product A to include (in hundreds of litres)

B = Amount of product B (in hundreds of litres) to include

Step 2: Objective function

Here we identify our objective as a function. In this case, we are aiming at choosing how to mix the products in order to minimize the cost. The function is therefore

Min Z=8A+ 7B

Step 3: Constrains

This step involves building up the constrains which our solution is confined within, they include;

There should be at least 4.5 litres of Orange and 5 liters of Mango in each 100L of the mixture therefore

(1) 6A +4B ≥ 4.5

(2) 4A +6B ≥ 5

There should be no more than 6 litres of Lime in each 100L of the mixture;

(3) 3A +8B ≤ 6

We should also meet the 70L demand per day so.

(4) A+B ≥ 0.70

Note: 70 was converted to 0.7 to match the other units which are in hundreds of litres

The non negativity constrains too should be included A and B should be greater than 0

(5) A ≥ 0,

(6) B≥ 0

ENROL WITH SIT718 REAL WORLD ANALYTICS ASSIGNMENT HELP AND HOMEWORK WRITING SERVICES OF EXPERTSMINDS.COM AND GET BETTER RESULTS IN SIT718 REAL WORLD ANALYTICS ASSIGNMENTS!

(c) Solution

For this part Desmos graphing calculator found online was used. Before using the calculator one should note;

(1) that the calculator shades on the solution areas with all our constrains functions the graph will look messy (with many colors) so during plotting I decided to flip the sign so that the shading is on outside the solution are leaving solution are not shaded.

(2) I used X to represent A and Y to represent B

The following solutions was obtained.

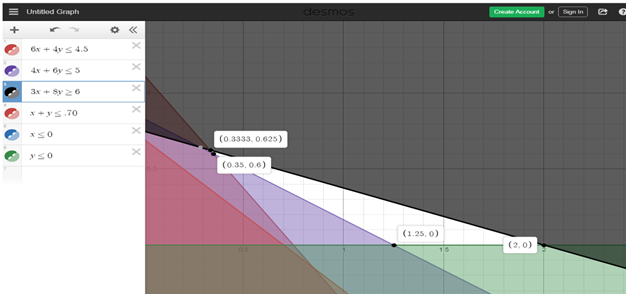
The following solutions was obtained; K(.3333, .625), L(.35,0.6), M(1.25,0),N(2,0), these values are in hundreds of liters cost corresponding to these points shown below;

Cost at K = 8(33.33) + 7(62.5) = 704.14

Cost at L = 8(35) + 7(60) = 700

Cost at M = 8(125) + 7(0) = 1000

Cost at N= 8(200) + 7(0) = 1600

Point L has the minimal cost hence the mixture should contain 35 litres of A and 60 litress of B

(d) Range of costs

The solution area is the area where we can operate without violating the constrains, the optimal solution in C above gives the minimum possible cost. Extreme values (maximum/minimum) of the solution(cost) happens at the corners (points K-M) therefore;

Operating on our solution area the maximum cost possible is 1600 (at point N) while the minimum cost happens all within the solution area our solution remains unchanged i.e all constrained are changed

The range is therefore

700 to 1600

24/7 AVAILABILITY OF TRUSTED SIT718 REAL WORLD ANALYTICS ASSIGNMENT WRITERS! ORDER ASSIGNMENTS FOR BETTER RESULTS!

Question 2 -

a) Formulate an LP model for the factory that maximises the profit, while satisfying the demand and the cotton and wool proportion constraints.

b) Solve the model using R/R Studio. Find the optimal profit and optimal values of the decision variables.

Answer -

Model formulation

Step 1: Decision variables

We have control over 3 variables in this problem; they include the 3 products produced. They include

X = the number of tones of spring produced

Y= the number of tones of Autumn produced

Z= the number of tones of winter produced

Step 2: objective function

The objective here is to maximize profits, from the given information we need to first calculate costs per ton per production, revenue and profit this was done in r to produce the outputs below;

Spring Autumn Winter

16.5 15 15.5

Step 3: The objective function is therefore

Max 16.5X + 15Y + 15.5Z

Step 3: Constrains

The constrains involved in this process are demand constrains and none negativity constrains only; the raw materials are not limited in this case. The constrains were formulated as follows;

(1) X ≤ 4500

(2) Y≤ 4000

(3) Z ≤ 4000

(4) X ≥ 0

(5) Y≥0

(6) Z ≥ 0

ORDER NEW SIT718 REAL WORLD ANALYTICS ASSIGNMENT AT NOMINAL PRICE!

Note: in this case the minimum requirements affect only the profit/costs per ton of production. They are therefore not constrains because there is no information about availability, the factory can produce any as many tons as it wants without raw materials being depleted.

Solution The r code for the solution is found on the appendix

The optimal decision is to produce the maximum number of demanded tons i.e 4500 tones of spring 4000 autumn and 4000 of winter

Step 3: Checking the constrains

By this rule the maximum demand is met; the material needed can be obtained by multiplying the demand and the required proportion per ton.

Code

code

require(lpSolveAPI)

# calculating profit perton -----------------------------------------------

cotton<-c(0.50,0.60,0.40);wool<-c(0.30,0.40,0.50);Purchase_Price<-c(30,45,50);sale_Price<-c(60,55,60);Production_cost<-c(5,4,5)

#minimums_requirement

minimums_requirement<-rbind(cotton,wool,silk=1-(cotton+wool))

colnames(minimums_requirement)<-c("Spring","Autumn","Winter")

minimums_requirement

#cost of materials

material_cost=minimums_requirement*Purchase_Price

material_cost

allmaterial_cost=colSums(material_cost)

#cost of materials+ production cost

costs<-rbind(allmaterial_cost,Production_cost)

costs

#overal cost of production

overal_cost<-colSums(costs)

overal_cost

#profit per ton

t(sale_Price-as.matrix(overal_cost))

#SOLUTION

model <- make.lp(3, 3)

lp.control(model, sense="max")

set.objfn(model, c(16.5,15,15.5))

add.constraint(model, c(1, 0,0), "<=", 4500)

add.constraint(model, c(0, 1,0), "<=", 4000)

add.constraint(model, c(0, 0,1), "<=", 4000)

add.constraint(model, c(1, 0,0), ">=", 0)

add.constraint(model, c(0, 1,0), ">=", 0)

add.constraint(model, c(0, 0,1), ">=", 0)

colnames(model)<-c("A","B","C")

model

solve(model)

##get the maximum profit

get.objective(lpmodel)

##get the solution

get.variables(lpmodel)

GET BENEFITTED WITH QUALITY SIT718 REAL WORLD ANALYTICS ASSIGNMENT HELP SERVICE OF EXPERTSMINDS.COM!

Question 3 -

(a) Give reasons why/how this game can be described as a two-players-zero-sum game.

(b) Formulate the payoff matrix for the game.

 (c) Explain what is a saddle point. Verify: does the game have a saddle point?

 (d) Construct a linear programming model for each player in this game;

(e) Produce an appropriate code to solve the linear programming model in part (c).

(f) Solve the game for David using the linear programming model you constructed in part (c). Interpret your solution.

Answer -

Formulating the payoff matrix

The raw payoff table is as follows

The payoffs were converted to non negative by adding a 2 to each entry of the matrix to get

(a) Saddle point

If two people are involved in Zero sum game max_i≤mmin_j≤na_ij ≤ min_i≤mmax_j≤n a_ij. But if the two are equal, I.e. max_i≤m min_j≤n a_ij = min_i≤m max_j≤n a_ij = V, V is the value of the game, the two players can each optimize their strategies. In such a condition the game is said to have a saddle point.

The minimum value s for the rows are (1, 0, 0, 0, 1, 0) the maximum of these minimums is 1.

The maximum value s for the columns are (2, 2, 2, 2, 2) the minimum of these minimums is 2.

Because the two are different there is no existence of a saddle point. The two players therefore cannot both optimize their strategies.

ORDER NEW COPY OF SIT718 REAL WORLD ANALYTICS ASSIGNMENT &AMP; GET HIGH QUALITY SOLUTIONS FROM SUBJECT'S TUTORS!

(b) Formulating linear programming model

Define the decision variables

The objective of the model would be to maximize the winning tendency (probability) for David with the 5 strategies the decision variables are the proportions (probability) with which David chooses each strategy with. The decision variables will be denoted as

X1 = probability with which she chooses strategy 1 with

X2 = probability with which she chooses strategy 2 with

X3 = probability with which she chooses strategy 3 with

X4 = probability with which she chooses strategy 4 with

X5= probability with which she chooses strategy 5 with

X5= probability with which she chooses strategy 5 with

Define the objective function

The Objective function for this case study is

Maximize x1+ x2+ x3 + x4 + x5 +x6 +x6

Define the Constrains

X₁ + 2X₂ + 2 X₃ + 2X₄ + X₅+ X₆

X₁ + X₂ + 2 X₃ + X₄ + X₅+ X₆

2X₁ + X₂ + X₄ +2 X₅ ++ X₆

2X₁ + X₂ + X₄ +2 X₅ ++ X₆

X₁ + 2X₂ + 2 X₃ + 2X₄ + X₅ + X₆

X₁ + X₂ + 2 X₃ + X₄ + X₅ + X₆

SAVE TOP GRADE USING SIT718 REAL WORLD ANALYTICS ASSIGNMENT HELP SERVICE OF EXPERTSMINDS.COM!

(a) The code produced

##Load the matrix

pay<-rbind(c(-1,0,0,0,-1),c(-1,-1,0,-1,-1),c(0,-1,-2,-1,0),c(0,-1,-2,-1,0),c(-1,-1,0,-1,-1),c(-1,0,0,0,-1))

pay

##Add two to make the payoff table non negative

pay<-pay+2

lpmodel <- make.lp(6, 5)

lp.control(lpmodel, sense="max")

set.objfn(lpmodel, c(1,1,1,1,1))

add.constraint(lpmodel, c(1, 2,2,2,1), "<=", 1)

add.constraint(lpmodel, c(1, 1,2,1,1), "<=", 1)

add.constraint(lpmodel, c(2,1,0,1,2), "<=", 1)

add.constraint(lpmodel, c(2,1,0,1,2), "<=", 1)

add.constraint(lpmodel, c(1, 1,2,1,1), "<=", 1)

add.constraint(lpmodel, c(1, 2,2,2,1), "<=", 1)

colnames(lpmodel)<-c("x1","x2","x3","x4","x5")

lpmodel

solve(lpmodel)

##get the optimal probability

get.objective(lpmodel)

##get the solution

get.variables(lpmodel)

(b) Solution

From the output David should choose strategy one 50% of the time avoid strategy 2, 4 and 5 completely choose strategy 3 25% of the time this way she has the potential to maximize expected winning 75%.

DO YOU WANT TO EXCEL IN SIT718 REAL WORLD ANALYTICS ASSIGNMENT - ORDER AT EXPERTSMINDS!

Avail best Deakin University, Australia Assignment Help Services at Expertsminds for its related courses and units, such as:

• SIT725 Software Engineering Assignment Help
• SIT740 Research and Development in Information Technology Assignment Help
• SIT764 Team Project (A) - Project Management and Practices Assignment Help
• SIT010 Safety Induction Program Assignment Help
• STP010 Career Tools for Employability Assignment Help
• SIT102 Introduction to Programming Assignment Help
• SIT103 Data and Information Management Assignment Help
• SIT105 Thinking Technology and Design Assignment Help
• SIT202 Networks and Communications Assignment Help
• SIT317 Enterprise, Entrepreneurship and Innovation Assignment Help