GET READYMADE REGRESSION ANALYSIS ASSIGNMENT SOLUTIONS - 100% PLAGIARISM FREE WORK DOCUMENT AT NOMINAL CHARGES!

Regression Analysis Assignment

Task B

Question 1. Calculate returns for these three series in Excel or any software of your choice using the transformation and perform the Jarque-Berra test of normally distributed returns for each of Boeing and GD. What do you infer about the distribution of the two stock returns series?

Solution.

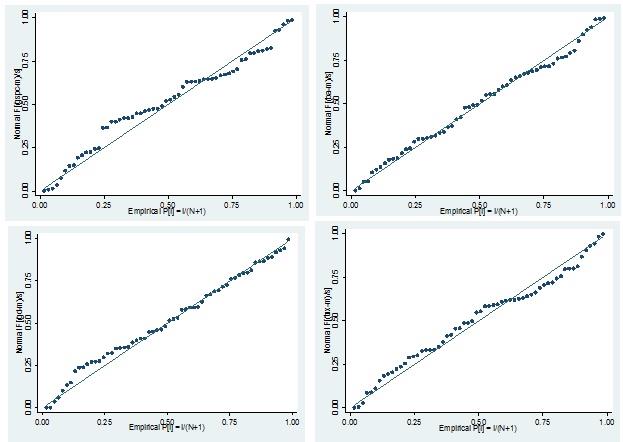
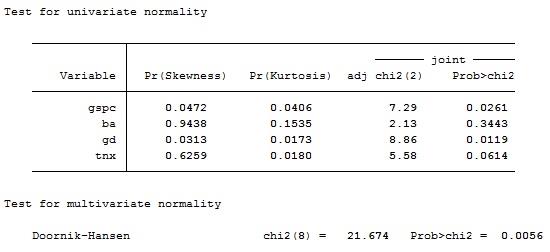
Along these lines, we see that the supposition of ordinariness isn't fulfilled

MOST RELIABLE AND TRUSTWORTHY REGRESSION ANALYSIS ASSIGNMENT HELP & HOMEWORK WRITING SERVICES AT YOUR DOORSTEPS!

Question 2. Test a hypothesis that the average return on GD stock is different from 2.8%. Which test statistic would you choose to perform this hypothesis test and why

Solution: So as to decide if the average GD stock is not the same as 2.8%, we perform one example t test. As per the Null and substitute theory, we can estimate that

H0: µ = 2.8% (Null Hypothesis)

That is, the average GD stock don't contrast essentially from 2.8%

Substitute Hypothesis: Ha: µ is not equal to 2.8%

That is, the average GD stock vary fundamentally from 2.8%

Dimension of Significance

Give the dimension of importance (a) = 0.05

Test Statistic

The t test measurement is  

t= (x ¯-μ)/(s/√n)=(-5.37-2.8)/(39.25/√60)=-1.613

Here, as per the t test, p - estimation is 0.112 which is greater than 0.05, demonstrating that there is no factual proof to dismiss the invalid speculation at 5% dimension of essentialness. In this manner, we don't have enough proof to infer that the average GD stock contrast essentially from 2.8%

Question 3. Before investing in one of the two stocks, you first want to compare risk associated with each of the two stocks. Perform an appropriate hypothesis test using 5% significance level and interpret your results.

Solution: So as to decide if there is any distinction in the average return between two stocks, we perform free example t test

H₀: µ₁ = µ₂  (As per the Null Hypothesis)

This implies that the average return between the two stocks don't contrast fundamentally

H_a: µ₁ ≠ µ₂  (As per the Substitute Hypothesis)

This implies that the average return between the two stocks vary appreciably

Dimension of Significance

Give the dimension of noteworthiness a chance to be α = 0.05

Test Statistic

As per the above table, which gives the t test, the p - estimation value is 0.216 which is greater than 0.05, demonstrating that there is no adequate proof to dismiss the invalid speculation at 5% dimension of essentialness. In this way, we reason that the average return between the two stocks vary fundamentally

SAVE DISTINCTION MARKS IN EACH REGRESSION ANALYSIS ASSIGNMENT WHICH IS WRITTEN BY OUR PROFESSIONAL WRITER!

Question 4. Perform an appropriate hypothesis test using information in your sample of 60 observations on returns. Report your findings and also mention which stock will you prefer and why?

Solution: So as to decide if there is any distinction in the average return between two stocks, we perform autonomous example t test

H₀: µ₁ = µ₂  (As per the Null Hypothesis)

This implies that the average return between the two stocks don't contrast essentially

H_a: µ₁ ≠ µ₂  (As per the Substitute Hypothesis)

This implies that the average return between the two stocks vary altogether

Dimension of Significance

Give the dimension of noteworthiness a chance to be α = 0.05

Test Statistic

As per the above mentioned table, which gives the t test measurement, the p-estimation value is 0.728 which is greater than 0.05, which depicts that we cannot violate the principles of Null Hypothesis (as the level of importance is nearly 5%). Along these lines, we infer that the average return between the two stocks contrast essentially

HIRE PROFESSIONAL WRITER FROM EXPERTSMINDS.COM AND GET BEST QUALITY REGRESSION ANALYSIS ASSIGNMENT HELP AND HOMEWORK WRITING SERVICES!

Question 5. Compute excess return on your preferred stock as yt = rt - rf,t and excess market return as xt = rM,t - rf,t and perform the following tasks.

Solution: The CAPM model yield is given beneath

a. From the above relapse yield, we have

Yt = - 0.00055 + 0.03821 * Xt

b. The coefficient of the free factor Xt is 0.03821, demonstrating that Yt increments by 0.03821 unit for each one unit increment in Xt

c. The coefficient of assurance is 0.0029, showing that 0.29% of the variety in the needy variable is clarified by the relapse model, while the staying 99.71% left unexplained

d. The 95% certainty interim for incline is (- 0.148, 0.224). This demonstrates, when rehashed tests are taken, at that point 95 out of multiple times the genuine slant esteem will fall inside this interim

Question 6. Using the confidence interval approach to hypothesis testing, perform the hypothesis test to determine whether your preferred stock is a neutral stock.

Solution: On observing the certainty interim esteem, we see that the esteem 0 falls inside the interim, showing that there is no valid reason to avoid the principles of Null speculation that the coefficient of the free factor don't vary essentially from zero. In this way, we have adequate proof to presume that the favored stock is an unbiased stock

WE HELP STUDENTS TO IMPROVE THEIR GRADES! AVAIL TOP QUALITY REGRESSION ANALYSIS ASSIGNMENT HELP AND HOMEWORK WRITING SERVICES AT CHEAPER RATE!

Question 7. Perform an appropriate hypothesis test to determine whether it is plausible to assume normally distributed errors.

Solution: Here, we can utilize histogram or ordinariness plot to decide if the mistakes pursue ordinary dispersion. Here, we utilize lingering plot to test the case

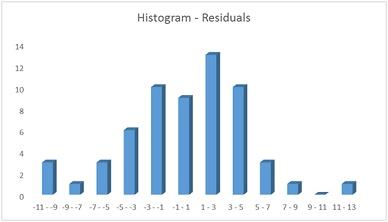
From the above plot, we see that the appropriation of residuals pursue ordinary conveyance around

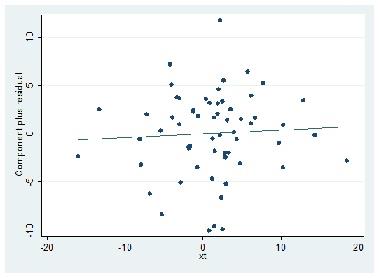
This residual plot indicates that the error distribution do not follow any pattern indicating that the error distribution is independent of each other.

NEVER MISS YOUR CHANCE TO EXCEL IN REGRESSION ANALYSIS ASSIGNMENT! AVAIL AFFORDABLE AND RELIABLE REGRESSION ANALYSIS ASSIGNMENTS HELP SERVICES OF EXPERTSMINDS.COM