MFE 6220 Quantitative Analysis in Equity Markets Assignment Help
Question 1
In class, we discussed the ACF formula for an MA(1) process without an intercept term. Now derive the ACF formula for an MA(1) process with the intercept term .
Question 2
Derive the ACF formula for an MA(2) process with the intercept term.
Question 3
A researcher studies data for the Chinese stock market returns series and finds that it can be modeled as an MA(3) process of the following form (where the standard errors are given in parentheses):
= 0.722 + 0.835 et-1 + 0.751 et-2 + 0.609 et-3
(0.289) (0.195) (0.201) (0.110)
; n = 185
a. Is the intercept term significant to the model? Conduct a relevant hypothesis test to answer this question.
b. What is the mean-reverting level for this data process?
c. Suppose the process is currently at . Then, in time period t a shock occurs to the system. In other words, . For simplicity, assume that there are no other shocks prior to or after this shock. Use relevant equations to trace the impact of this shock from period (t-1) to (t+k).
d. Based on your findings in part (c), show that the above MA(3) process has finite memory. In other words, the impact of the shock fully dissipates after a finite number of periods and the data process will get back to its mean-reverting level that you obtained in part (b).
e. Suppose the researcher’s advisor says, that fifty years ago, the true underlying data generating process for the Chinese stock returns series was in fact an MA(1) process shown by Yt = εt + 0.65 εt-1.
Draw a plot of the Autocorrelation Function (ACF) for this MA(1) process up to 4 lags.
Getting Stuck with Similar Assignment? Enrol with Expertsminds’ XMFE 6220 Quantitative Analysis in Equity Markets Assignment Help services now!
Question 1
In class, we discussed the ACF formula for an MA(1) process without an intercept term. Now derive the ACF formula for an MA(1) process with the intercept term.
The model is
ACF: Yt = d + ? Yt-1 + ?t where |? < ?
Thus, we see that
It = { = Y-∞, ....., Yt} represents the mean optimal forecast
?1 = Y1 - µ - α ?0
On going till n times, we see that
?t = Yt - µ - α ?t-1 = f0¬ (Y0, .... Yt)
Question 2
Derive the ACF formula for an MA(2) process with the intercept term.
The model is
ACF: Yt = d + ? Yt-1 + ?t where |? < ?
Thus, we see that
It = { = Y-∞, ....., Yt} represents the mean optimal forecast
Here, ACF formula for an MA(2) process with the intercept term
X(t) = a + b*X(t-1)
x(t)-x(t-1)=a+bx(t-1)
x(t)=x(t-1)=x
(1-b)x=a
x=a/(1-b)
Question 3
A researcher studies data for the Chinese stock market returns series and finds that it can be modeled as an MA(3) process of the following form (where the standard errors are given in parentheses):
= 0.722 + 0.835 et-1 + 0.751 et-2 + 0.609 et-3
(0.289) (0.195) (0.201) (0.110)
; n = 185
a. Is the intercept term significant to the model? Conduct a relevant hypothesis test to answer this question.
Here, the value of test statistic is 2.498 and its corresponding p - value is 0.014 < 0.05, indicating that the intercept term is statistically significant
b. What is the mean-reverting level for this data process?
Here, we see that the mean reverting level µ set to 0.5
c. Suppose the process is currently at . Then, in time period t a shock occurs to the system. In other words, . For simplicity, assume that there are no other shocks prior to or after this shock. Use relevant equations to trace the impact of this shock from period (t-1) to (t+k).
Here, the process is currently at µ is 5.035 and its corresponding p - value is 0.000 < 0.05, which shows a clear indication that the t time period t a shock that occurs to the system.
The lag operator is distributive over the addition operator, i.e
L(xt + yt) = xt-1 + yt-1
d. Based on your findings in part (c), show that the above MA(3) process has finite memory. In other words, the impact of the shock fully dissipates after a finite number of periods and the data process will get back to its mean-reverting level that you obtained in part (b).
The MA (1) process is given below
t=εt+θεt-1
γ(0)=σ2(1+θ2),γ(1)=σ2θ,andγ(k)=0∀k>1
Here, ACF formula for an MA(3) process with the intercept term
X(t) = a + b*X(t-1)
x(t)-x(t-1)=a+bx(t-1)
x(t)=x(t-1)=x
(1-b)x=a
x=a/(1-b)
Now, the required mean reverting level is found to be 0.7
e. Suppose the researcher's advisor says, that fifty years ago, the true underlying data generating process for the Chinese stock returns series was in fact an MA(1) process shown by Yt = εt + 0.65 εt-1.
The model is
ACF: Yt = d + ? Yt-1 + ?t where |? < ?
Thus, we see that
It = { = Y-∞, ....., Yt} represents the mean optimal forecast
Here, we see that
Yt = εt + 0.65 εt-1
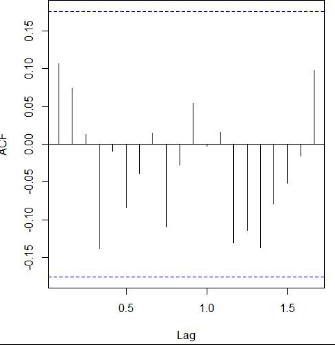
Draw a plot of the Autocorrelation Function (ACF) for this MA(1) process up to 4 lags.
An ACF graph example for this MA (1) process up to 4 lags is given below
Never be caught in plagiarism, Avail MFE 6220 Quantitative Analysis in Equity Markets Assignment Help service of Expertsminds.com and save higher marks!