GET ASSURED A++ GRADE IN EACH MEPM 531 INTEGER LINEAR PROGRAMMING ASSIGNMENT ORDER - ORDER FOR ORIGINALLY WRITTEN SOLUTIONS!
MEPM 531 Operation Research Assignment - Integer Linear Programming, American University of Ras Al Khaimah, UAE
Q1. Solve the following integer linear programming problem by using:
a) Branch and Bound Method
Problem is: Max Z = 3x1 + 4x2
Subject to 2x1+ x2 ≤ 6
2x1 + 3x2 ≤ 9
X1, X2 ≥ 0, and integers
Solution in 4 parts:
Part 1: To draw constraint 2x1+ x2 ≤ 6 → (1)
2x1+ x2 ≤ 6
Treat it as 2x1+ x2 = 6
When x1 = 0 then x2 =?
2(0) + x2 = 6
x2 = 6
When x2 = 0 then x1 =?
2x1 + 0 = 6
x1 = 6/2 = 3
Part 2: To draw constraint 2x1+ 3x2 ≤ 9 → (2)
2x1 + 3x2 ≤ 9
Treat it as 2x1 + 3x2 = 9
When x1 = 0 then x2 = ?
2(0) + 3 x2 = 9
3 x2 = 9
x2 = 9/3 = 3
When x2 = 0 then x1 =?
2x1 + 3 (0) = 9
2x1 = 9
x2 = 9/2 = 4.5
NO PLAGIARISM POLICY - ORDER NEW MEPM 531 INTEGER LINEAR PROGRAMMING ASSIGNMENT & GET WELL WRITTEN SOLUTIONS DOCUMENTS WITH FREE TURNTIN REPORT!
Part 3: To draw constraint >= 0 → (3)
Treat it as = 0
Equation is not possible.
Part 4: To draw constraint >= 0 → (4)
Treat it as = 0
Equation is not possible.
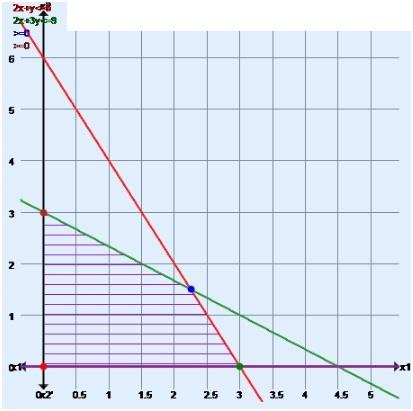
The value of the objective function at each of these extreme points is as follow:
|
Extreme Point Coordinates (x1, x2)
|
Line through Extreme Point
|
Objective function value Z = 3x1+ 4x2
|
|
O(0,0)
|
5→ x1 >= 0
6→ x2 >= 0
|
3(0) + 4(0) = 0
|
|
A(3, 0)
|
1→ 2 x1 + x2 <= 6
6→ x2 >= 0
|
3(3) + 4(0) = 9
|
|
B(9/4, 3/2)
|
1 → 2 x1 + x2 <= 6
2 → 2 x1 + 3x2 <= 9
|
3(9/4) + 4(3/2) = 51/4
|
|
C(0,3)
|
2 → 2 x1 + 3x2 <= 9
5 → x1 >= 0
|
3(0) + 4(3) = 12
|
The maximum value of the extreme function Z = 51/4 occurs at the extreme point (9/4, 3/2). Hence, the optional solution to the given LP problem is: x1 = 94, x2 =32 and max Z = 51/4.
b) Fractional Cut Method
Problem is:
Max Z = 3x1+ 4x2
Subject to 2x1+ x2 ≤ 6
2x1+ 3x2 ≤ 9
X1, X2 ≥ 0, and integers
Standard form
Z = 3x1+ 4x2 + 0S1 + 0S2
S. t.
2x1+ x2 + S1 = 6
2x1+ 3x2 + S2 = 9
X1, X2, S1, S2 >= 0
IBFS
S1 = 6 and S2 = 9
Cj (3 4 0 0)
|
CB
|
YB
|
XB
|
Y1*
|
Y2
|
Y3
|
Y4
|
|
0
|
Y3
|
6
|
2
|
2
|
1
|
0
|
|
0
|
Y4
|
9
|
2
|
3
|
0
|
1
|
CB X Y1 CB X Y2 + CB X Y3
Zj 0X2 = 0, 0 X 2 + 0X3 = 0; 0 0
0 0 0 0
Net Evaluation Zj - Cj -3 -4 0 0
Net Evaluation not >= 0
Most negative -4, arbitrary we select Y1 enters basis.
Min {XB/Y1j} = min {6/2, 9/2} 6/2 Y3 Leave basis
Cj (3 4 0 0)
|
CB
|
YB
|
XB
|
Y1*
|
Y2
|
Y3
|
Y4
|
|
1
|
Y1
|
6/6 = 1
|
2
|
2
|
1
|
0
|
|
0
|
Y4
|
9
|
2
|
3
|
0
|
1
|
CB X Y1 CB X Y2 + CB X Y3
Zj 0X2 = 0, 0 X 2 + 0X3 = 0; 0 0
0 0 0 0
Net Evaluation Zj - Cj -3 -4 0 0
Net Evaluation not >= 0
Most negative -4, arbitrary we select Y1 enters basis.
Min {XB / Y1j} = min {6/2, 9/2} 6/2 Y3 Leave basis
|
CB
|
YB
|
XB
|
Y1*
|
Y2
|
Y3
|
Y4
|
|
1
|
Y1
|
6/6 = 1
|
2/2 = 1
|
2/2 = 1
|
½
|
0
|
|
0
|
Y4
|
9/3 = 3
|
2/3
|
3/3 = 3
|
0/3 = 0
|
1/3
|
CB X Y1 CB X Y2 + CB X Y3
Zj 0X2 = 0, 0 X 2 + 0X3 = 0; 0 0
0 0 0 0
Net Evaluation Zj - Cj 1 3/2 0 0
Net Evaluation not >= 0
Most negative -4, arbitrary we select Y1 enters basis.
Min {XB/Y1j} = min {1, 3/2} 6/2 Y4 Leave basis.
ENDLESS SUPPORT IN MEPM 531 INTEGER LINEAR PROGRAMMING ASSIGNMENTS WRITING SERVICES - YOU GET REVISED OR MODIFIED WORK TILL YOU ARE SATISFIED WITH OUR MEPM 531 INTEGER LINEAR PROGRAMMING ASSIGNMENT HELP SERVICES!
Q2. Solve the following integer linear problem by:
a) Branch and Bound Method
Max Z = 4x1 + 6x2+ 2x3
s.t. 4x1 - 4x2 ≤ 5
-x1 + 6x2 ≤ 5
-x1 + x2 + x3 ≤ 5
x1, x2, x3 ≥ 0 and integers
Part 1: To draw constraint 4x1 - 4x2 ≤ 5 → (1)
4x1 - 4x2 ≤ 5
Treat it as 4x1 - 4x2 = 5
When x1 = 0 then x2 =?
4(0) - 4x2 = 5
- 4x2 = 5
x2 = -5/4 = -1.25
When x2 = 0 then x1 =?
4x1 - 4(0) = 5
4x1 = 5
x1 = 5/4 = 1.25
Part 2: To draw constraint -x1+ 6x2 ≤ 5 → (2)
-x1 + 6x2 ≤ 5
Treat it as -x1 + 6x2 = 5
When x1 = 0 then x2 =?
-1(0) + 6x2 = 5
6x2 = 5
x2 = 5/6
When x2 = 0 then x1 = ?
-x1 + 6(0) = 5
-x1 = 5
x1 = -5
HELPING STUDENTS TO WRITE QUALITY MEPM 531 INTEGER LINEAR PROGRAMMING ASSIGNMENT AT LOW COST!
Part 3: To draw constraint -x1+ x2+ x3 ≤ 5 → (3)
-x1+ x2+ x3 ≤ 5
Treat it as -x1+ x2+ x3 = 5
When x1 = 0 then x2 = -4/5 from equation (1)
Then -x1+ x2+ x3 = 5
-1(0) + -4/5 + x3 = 5
x3 = 5 + 4/5 = 29/5
When x2 = 0 then x1 = 5/4 from equation (1)
-x1+ x2+ x3 = 5
-(5/4) + 1(0) + x3 = 5
-(5/4) + x3 = 5
x3 = 5 + 5/4 = 25/4
When x1 = 0 then x2 = 5/6 from equation (2)
Then -1 (0)+ 5/6 + x3 = 5
5/6 + x3 = 5
x3 = 5 - 5/6 = 5
When x2 = 0 then x1 = 5/6 from equation (2)
-5/6 + 1(0) + + x3 = 5
-(5/6) + x3 = 5
x3 = 5 -(5/6) = 25/6
|
x1 = 0, x2 = -4/5 then
|
x3
|
29/5
|
|
x2 = 0 , x1 =5/4 then
|
x3
|
25/4
|
|
x1 = 0, x2 = 5/6 then
|
x3
|
5
|
|
x2 = 0 x1 = 5/6
|
x3
|
25/6
|
GET READYMADE MEPM 531 INTEGER LINEAR PROGRAMMING ASSIGNMENT SOLUTIONS - 100% PLAGIARISM FREE WORK DOCUMENT AT NOMINAL CHARGES!
b) Fractional Cut Method
Max Z = 4x1+ 6x2 + 2x3
s.t. 4x1 - 4x2 ≤ 5
-x1 + 6x2 ≤ 5
-x1 + x2+ x3 ≤ 5
x1, x2, x3 ≥ 0 and integers
Standard form
Z = 4x1 + 6x2 + 2x3
s.t. 4x1- 4x2 ≤ 5
-x1 + 6x2 ≤ 5
-x1 + x2+ x3 ≤ 5
x1, x2, x3 ≥ 0 and integers
IBFS
S1 = 5 and S2 = 5
Cj (4 6 0 0)
|
CB
|
YB
|
XB
|
Y1*
|
Y2
|
Y3
|
Y4
|
|
0
|
Y3
|
5
|
4
|
-2
|
2
|
0
|
|
0
|
Y4
|
5
|
3
|
3
|
0
|
1
|
CB X Y1 CB X Y2 + CB X Y3
Zj 0X2 = 0, 0 X 2 + 0X3 = 0; 0 0
0 0 0 0
Net Evaluation Zj - Cj -8 -7 0 0
Net Evaluation not >= 0
Most negative -4, arbitrary we select Y1 enters basis.
Min {XB / Y1j} = min {6/2, 9/2} 6/2 Y3 Leave basis
Cj (3 4 0 0)
|
CB
|
YB
|
XB
|
Y1*
|
Y2
|
Y3
|
Y4
|
|
1
|
Y1
|
6/7
|
2
|
2
|
1
|
0
|
|
0
|
Y4
|
8/7
|
2
|
3
|
0
|
1
|
CB X Y1 CB X Y2 + CB X Y3
Zj 0X2 = 0, 0 X 2 + 0X3 = 0; 0 0
0 0 0 0
Net Evaluation Zj - Cj -3 -4 0 0
Net Evaluation not >= 0
Most negative -4, arbitrary we select Y1 enters basis.
Min {XB / Y1j} = min {5/2, 3/2} 5/2 Y3 Leave basis
|
CB
|
YB
|
XB
|
Y1*
|
Y2
|
Y3
|
Y4
|
|
1
|
Y1
|
6/3 = 3
|
2/2 = 1
|
2/2 = 1
|
1/2
|
0
|
|
0
|
Y4
|
9/3 = 3
|
2/3
|
3/3 = 3
|
0/3 = 0
|
1/3
|
CB X Y1 CB X Y2 + CB X Y3
Zj 0X2 = 0, 0 X 2 + 0X3 = 0; 0 0
0 0 0 0
Net Evaluation Zj - Cj 1 3/2 0 0
Net Evaluation not >= 0
Most negative -4, arbitrary we select Y1 enters basis.
Min {XB / Y1j} = min {7, 5/2} 5/2 Y4 Leave basis.
MOST RELIABLE AND TRUSTWORTHY MEPM 531 INTEGER LINEAR PROGRAMMING ASSIGNMENT HELP & HOMEWORK WRITING SERVICES AT YOUR DOORSTEPS!
3) Solve the following integer linear problem by:
a) Branch and Bound Method
Max Z = 3x1 + x2 + 3x3
s. t. - x1 + 2x2 + x3 ≤ 4
4x2 - 3x3 ≤ 2
x1 - 3x2 + 2x3 ≤ 3
x1, x2, x3 ≥ 0 and integers
Solution: To apply branch and bound method, the three constraints to be added to LP model.
x1 <= 1
x2 <= 1
x3 <= 1
Solution Steps by Big M method:
Max Z = 3x1 + x2 + 3x3
s. t. - x1 + 2x2 + x3 ≤ 4
4x2 - 3x3 ≤ 2
x1 - 3x2 + 2x3 ≤ 3
x1, x2, x3 ≥ 0
Solution is:
Max Z A = 7 (x1= 1, x2 = 1, x3 = 1)
and ZL = 7 (x1= 1, x2 = 1, x3 = 1) obtained by the rounded off solutions value.
This problem has integer solution, so no further branching is required.
The branch and bound diagram.
A
x1= 1, x2 = 1, x3 = 1
ZA = 7
ZL = 7
Solution steps by Big M method.
The 0-1 Integer Programming problem algorithm thus terminated and the optimal integer solution is: ZA = 7 and x1= 1, x2 = 1, x3 = 1
SAVE DISTINCTION MARKS IN EACH MEPM 531 INTEGER LINEAR PROGRAMMING ASSIGNMENT WHICH IS WRITTEN BY OUR PROFESSIONAL WRITER!
b) Fractional Cut Method
Standard form
Max Z = 3x1 + x2 + 3x3
s. t. - x1 + 2x2 + x3 ≤ 4
4x2 - 3x3 ≤ 2
x1 - 3x2 + 2x3 ≤ 3
x1, x2, x3 ≥ 0 and integers
IBFS
S1 = 0 and S2 = 3
Cj (4 6 0 0)
|
CB
|
YB
|
XB
|
Y1*
|
Y2
|
Y3
|
Y4
|
|
0
|
Y3
|
0
|
2
|
4
|
2
|
0
|
|
0
|
Y4
|
3
|
1
|
3
|
3
|
1
|
CB X Y1 CB X Y2 + CB X Y3
Zj 0X2 = 0, 0 X 2 + 0X3 = 0; 0 0
0 0 0 0
Net Evaluation Zj - Cj 10 13 0 0
Net Evaluation not >= 0
Most negative -4, arbitrary we select Y1 enters basis.
Min {XB / Y1j} = min {1/2, 4/2} 1/2 Y3 Leave basis
Cj (3 4 0 0)
|
CB
|
YB
|
XB
|
Y1*
|
Y2
|
Y3
|
Y4
|
|
1
|
Y1
|
3/2
|
3
|
2
|
1
|
0
|
|
0
|
Y4
|
6/3
|
5
|
3
|
0
|
1
|
CB X Y1 CB X Y2 + CB X Y3
Zj 0X2 = 0, 0 X 2 + 0X3 = 0; 0 0
0 0 0 0
Net Evaluation Zj - Cj -3 -4 0 0
Net Evaluation not >= 0
Most negative -4, arbitrary we select Y1 enters basis.
Min {XB / Y1j} = min {5/2, 3/2} 5/2 Y3 Leave basis
|
CB
|
YB
|
XB
|
Y1*
|
Y2
|
Y3
|
Y4
|
|
1
|
Y1
|
6/3 = 3
|
2/2 = 1
|
2/2 = 1
|
1/2
|
0
|
|
0
|
Y4
|
9/3 = 3
|
2/3
|
3/3 = 3
|
0/3 = 0
|
1/3
|
CB X Y1 CB X Y2 + CB X Y3
Zj 0X2 = 0, 0 X 2 + 0X3 = 0; 0 0
0 0 0 0
Net Evaluation Zj - Cj 1 3/2 0 0
Net Evaluation not >= 0
Most negative -4, arbitrary we select Y1 enters basis.
Min {XB / Y1j} = min {8, 3/5} 3/5 Y4 Leave basis.
NEVER MISS YOUR CHANCE TO EXCEL IN MEPM 531 INTEGER LINEAR PROGRAMMING ASSIGNMENT! AVAIL AFFORDABLE AND RELIABLE MEPM 531 INTEGER LINEAR PROGRAMMING ASSIGNMENTS HELP SERVICES OF EXPERTSMINDS.COM!
Avail the best American University of Ras Al Khaimah, UAE Assignment Help for below mentioned units and courses:-
- MEPM 519 Field Application Project Assignment Help
- MEPM 521 Project Cost Accounting and Finance Assignment Help
- MEPM 523 Direct Research Assignment Help
- MEPM 532 Engineering Management Assignment Help
- MEPM 541 Organization Behavior and Project Team Management Assignment Help
- MEPM 543 Risk Management for Project Managers Assignment Help
- MEPM 513 Project Implementation and Performance Assignment Help
- MEPM 514 Global Projects Management Assignment Help
- MEPM 516 Project Quality Management Assignment Help
- MEPM 522 Financial Analysis and Decision Making Assignment Help
- MEPM 533 Information Systems for Project Management Assignment Help
- MEPM 542 Supply Chain Management for Project Managers Assignment Help