DO YOU WANT TO EXCEL IN LONG RUN PRODUCTION ASSIGNMENT - ORDER AT EXPERTSMINDS!

Case Study: Long-run Production

Section 1

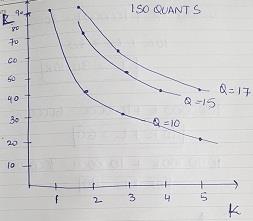
a) Graph isoquants for production of 10, 15, and 17

Answer:  The following is the isoquant:

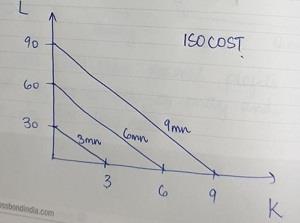
b) If prototyping facilities cost $1,000,000 and engineers cost $100,000, then graph the isocost curves associated with costs of $3 million, $6 million, and $9 million.

Answer:

The following is the iso-cost curves:

1000000K + 100000L = 3000000

10 K  + L = 30

L = 30 - 10 K

1000000 K + 100000L = 6000000

10K + L = 60

1000000 K + 100000 L = 9000000

10K + L = 90

ORDER NEW LONG RUN PRODUCTION ASSIGNMENT & GET 100% ORIGINAL SOLUTION AND QUALITY WRITTEN CONTENTS IN WELL FORMATS AND PROPER REFERENCING.

Section 2 Cost Minimization and the Last Dollar Rule

a) Find the function for the marginal product of labor and the function for the marginal product of capital.

Answer: The following are the marginal cost of labor and capital:

MP_L= ∂Q/∂L = 2*0.6*K^0.5 L^-0.4 = 1.2K^0.5 L^-0.4
MP_K= ∂Q/∂K = 2*0.5*K^-0.5 L^0.6 = K^-0.5 L^0.6

b) Use the marginal products that you just found and the wage of $100,000 and the rental rate of $1,000,00 to determine if the last dollar rule is satisfied when there are 50 engineers (L) and 2 prototyping facilities (K).

Answer:

The wage to rental ratio is as follows:

w/r=100000/1000000=0.1

At K=2 and L=50,

MP_L/MP_K = 1.2KL^-1 = 1.2*2*50^-1 = 0.048

The firm should use more prototyping facilities i.e. should use more K as 0.0048 is less than 0.1.

c) Use a Lagrangian (or another method) to find the optimal combination of capital and labor when the budget is $11 million. The budget is $11,000,000.

Answer:

Maximise

Q=2*K^0.5 L^0.6

w.r.t:

11000000=100000L+1000000K

Using Lagrange's equation:

L_a = 2*K^0.5 L^0.6-λ(100000L+1000000K-11000000)

∂La/∂K=K^-0.5 L^0.6 - 1000000λ = 0

∂La/∂L = 1.2K^0.5 L^-0.4 - 100000 λ = 0

∂La/∂λ = 100000L + 1000000K -  11000000 = 0

L + 10K = 110

L = 110 - 10K

K^-0.5 L^0.6/1000000 = 1.2K0.5 L^-0.4/100000

12 = K^-1 L¹

L=12K

22K=110

K=110/22=5

L=12K=12*5=60

d) Use a Lagrangian (or another method) to find the optimal combination of capital and labor to reach a production target of 50.

Answer:

The budget production is 50.
Minimise:
C=100000L+1000000K
Subject to:
50=2*K^0.5 L^0.6
Using Lagrange's equation:
La=100000L+1000000K-λ(2*K^0.5 L^0.6-50)
∂La/∂K=1000000-λK^(-0.5) L^0.6=0
∂La/∂L=100000-1.2λK^0.5 L^(-0.4)=0
∂La/∂λ=2*K^0.5 L^0.6-50=0

K^0.5 L^0.6=25
100000/(1.2K^0.5 L^(-0.4) )=1000000/(K^(-0.5) L^0.6 )
L=12K

K^0.5 (12K)^0.6=25
K=6.69 or 7
L=12*7=84

GETTING STUCK WITH SIMILAR LONG RUN PRODUCTION ASSIGNMENT? ENROL WITH EXPERTSMINDS'S LONG RUN PRODUCTION ASSIGNMENT HELP SERVICES AND GET DISTRESSED WITH YOUR ASSIGNMENT WORRIES!

Section 3. The Expansion Path and Long-run Costs

Answer:

a) The cost of labor is $100 and the cost of capital is $500. Graph the isocost curves and some possible isoquants that correspond to these outputs and the optimal input bundles.

Answer: The following are the expansion path, isocost and isoquant lines:

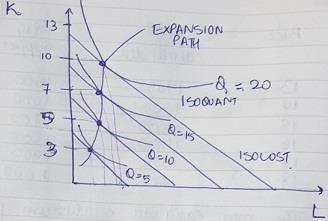
b) Find the long-run average cost for each of these outputs

Answer: The following is the long run average cost:

c) Economies of scale exist over what range of outputs?

Answer: The economies of scale exist when long run average cost decreases as output increases. It exists for output 5 units to 15 units. The diseconomies of scale exist when long run average cost increases as output increases. It exists for output 15 units to 25 units.

Section 4. Forces Affecting Long-run Costs

Answer:

a) Explain why a production process may have economies of scale

Answer: A production process may have economies of scale if the production process has a scope for division of labor and specialization. A single person doing the entire work is tedious and involves cost. Hence, in the large firm, people are employed to specialize in their respective task, thus, making huge production and achieving lower average cost with increasing output.

b) Explain why a production process may have diseconomies of scale.

Answer: A production process may have diseconomies of scale because of the inefficiency of the management to delegate the work and efficiency of the operation is lost. Hence, the long run average cost increases as the output increases.

c) Explain why a production process may have economies of scope.

Answer: A production process may have economies of scope as multiple goods are produced together as joint products. Joint products are the goods employing resources to produce one good causes one or more other goods to be produced as by-products at little or no additional cost. Example of joint product is beef carcasses and the leather products produced with hides that are by-products of beef production.

d) Explain why a production process may have purchasing economies of scale.

Answer: A production process may have purchasing economies of scale because the large-scale purchasing of raw materials helps the large buyers to obtain lower input prices through quantity discounts. At the threshold level of output where a firm buys enough of an input to qualify for quantity discounting, the firm's LAC curve shifts downward. Purchasing economies are common for advertising media, some raw materials, and energy supplies.

SAVE YOUR HIGHER GRADE WITH ACQUIRING LONG RUN PRODUCTION ASSIGNMENT HELP & QUALITY HOMEWORK WRITING SERVICES OF EXPERTSMINDS.COM